When we get to other worlds how will we get from point A to B? There are no roads on Ceres. No rivers or oceans on the moon. No airports on Enceladus or even air for an airplane to glide on.
Until transportation infrastructure is built, suborbital hops seem the way to go. A suborbital hop is an ellipse with a focus at the body center. But with much of the ellipse below surface.
For a suborbital hop from A to B, how much velocity is needed? At what angle should we leave the body's surface? At what angle and velocity do we return?
Points A and B are two points in a Lambert Space Triangle. The triangle's third point C is the body's center.
Two of the sides are radii of a spherical body so the triangle is isosceles.
A point's distance from one focus plus distance to second focus is a constant, 2a. 2a is the ellipse's major axis. Since A and B are equidistant to the first focus, they're also equidistant to the second focus. Points A & B, the planet and ellipse are all symmetric about the ellipse's axis.
The payload returns to the body at the same angle and velocity it left.
There are a multitude of ellipses whose focus lies at the center and pass through points A and B. How do we find the ellipse that requires the least delta V?
Specific orbital energy is denoted ε.
ε = 1/2 v2 - μ/r.
1/2 v2 is the specific kinetic energy from the body's motion. - μ/r is the specific potential energy that comes from the object's distance from C, the body's center. For an elliptic orbit, | - μ/r | is greater than 1/2 v2, that is the potential energy overwhelms the kinetic energy. If potential and kinetic energy exactly cancel, the orbit is parabolic and the payload's moving escape velocity.
So to minimize 1/2 v2 we'd want to maximize | ε |.
It so happens that
ε = - μ/(2 a).
To grow |- μ/(2 a)| we shrink 2a. So we're going for the ellipse with the shortest possible major axis.
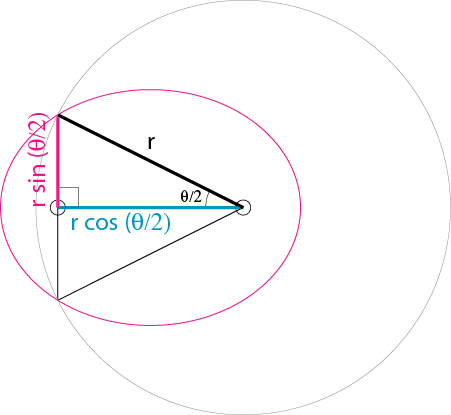
The foci of all these ellipses lie on the same line. Moving the focus up and down this line, it can be seen the ellipse having the shortest major axis has a focus lying at the center of the chord connecting A and B. That would be the red ellipse pictured above.
The angle separating A and B is labeled θ. Recall the black length and red length sum to 2a
2a = r + r sin(θ/2).
a = r(1 + sin(θ/2))/2.
Now that we know a, we can find velocity with the vis-viva equation:
V = sqrt(μ(2/r - 1/a)).
At what angle should we fire the payload?
It's known a light beam sent from one focus would be reflected to the second focus with the angle of incidence equal to the angle of reflection:
Angle between position vector and velocity vector is (3π - θ)/4. A horizontal velocity vector has angle π/2 from the position vector.
(3π - θ)/4 - π/2 = (3π - θ)/4 - 2π/4 =
(π - θ)/4
(π - θ)/4 is the flight path angle departing from point A. If A and B are separated by 180º (i.e. travel from north pole to south pole), flight path angle is 0º and the payload is fired horizontally. If A and B are separated by 90º (i. e. travel from the north pole to a location on the equator), flight path angle is (180º - 90º)/4 which is 22.5º
When A and B are very close, θ is close to 0. (180-0)/4 is 45º. When A and B are close the the payload would be fire at nearly 45º. With one focus near to the surface and the other at the body center, the ellipse would have an eccentricity of almost 1. The trajectory would look parabolic.
Here's a few possible suborbital hops on our moon:
Minimum energy ellipse from pole to pole is a circle. Launch velocity is about 1.7 km/s. It'd take the same amount of delta V for a soft landing at the destination. Trip time would be about 54 minutes
From the north pole to the equator would take a 1.53 km/s launch. Trip time would be about 27 minutes.
Period of a circular orbit (T) is 2 π * sqrt(r3/(Gm)) where m is mass of planet.
Mass can be expressed as ρ * volume where ρ is density.
2 π * sqrt(r3/Gm) = 2 π * sqrt(r3/(G * 4/3 *π * r3 * ρ).
The r3 cancels out and we're left with T = sqrt(π/(G * 4/3 * ρ).
Thus trip times for a given separation rely solely on density. Period scales with inverse square root of density.
I did a spreadsheet where the user can enter angular separation on various airless bodies in our solar system. Delta Vs vary widely depending on size of the bodies. But trip times between comparable angular separations are roughly the same. This is because most the bodies have roughly the same density. Denser bodies like Mercury will have shorter trip times while icey, low density bodies will have longer trip times.
I got some help on this from a Nasa Spaceflight thread. My thanks to AlanSE and Proponent.
After time we would establish infrastructure on bodies and burrow into their volume. With tunnels we could reach various destinations with very little energy. I look at this in Travel On Airless World Part II.






9 comments:
Luna spins very slowly, but surface speed of some bodies could be a significant fraction of circular speed. How does that affect the analysis?
An equator to equator hop is one thing, but most hops would require a change of orbital planes.
- MBMelcon
Good observation Melcon37. Yes, my simple model assumes non spinning bodies. On spinning bodies like Ceres you'd have to aim ahead of where the destination is at time of launch. Sort of like a duck hunter will aim at a location in front of a flying duck. A spinning world complicates things considerably.
Thanks for that calculation. These speeds are so low they could easily be done by a reusable single stage vehicle, such as the lunar transports in 2001: A Space Odyssey.
Bob Clark
Bob, indeed. Top delta V budgets between distant lunar points would be would be around 3 or 4 km/s.
And it could be even less.
I initially thought of this when considering travel from the Lunar Whipple crater to the equator. Or from Shackleton crater to the equator. I like to imagine magrails connecting various locations within these craters. Magrails going up the slopes of these craters might provide some of the lift off delta V.
A stripped down Dragon with superDraco engines could weigh 7 000 lbs dry plus 8 000 lbs fuel and have an Isp of 235 seconds. This would mean a delta-V of 1750 m/s. (Not my own numbers or calculation). That would be almost precesely enough to jump between any two points on the Moon. Or is this incorrect?
A jumping lunar Dragon could move to stay in sunlight during an entire month and do terrific science on multiple sites. And it would be an affordable project in a couple of years with a modified reused Dragon on a Falcon 9R.
I recommend this recent presentation of NASA's plans for "Red Dragon" to Mars:
https://www.youtube.com/watch?v=ZoSKHzziLKw&feature=youtu.be
In a recent blog comments exchange, someone stated that the DV for supplying an equatorial lunar base is lower from an asteroid than it would be from a lunar pole because a suborbital hop involves boost and deceleration whereas an asteroid ion pushed to LLO would only require deceleration at the lunar surface. When Iooked into it I was surprised to find that this might be correct. By my eyeballing it, it seems that anything higher than 40 degrees latitude would favor the poles and anything equatorial to 40 degrees would favor sourcing from and asteroid. Can you confirm or invalidate that?
Doug, sounds about right to me. A payload from some of the more accessible near earth asteroids would strike the moon at around 2.5 km/s. However launch windows to and from such asteroids would be on the order of years or even decades apart. I don't see a near earth asteroid in heliocentric orbit as a practical supplier to any moon base.
One of my day dreams at the moment are asteroids parked in high lunar orbits. Parking a rock in 30,000 km altitude polar orbit 30,000 km is well above the mascons that destabilize low lunar orbits. And it's deep enough in the lunar gravity well that tidal influences from the earth and sun don't wreck the orbit.
Extend tethers of modest length moonwards from the rock and you can drop payloads to the moon that would impact at less than lunar escape velocity. Extend tethers of modest length outwards and you can fling payloads to EML2.
Extend the tether foot to just above the lunar surface and payloads at be dropped at much slower velocity. Longer tethers outwards could fling payloads to trans LEO orbits or into heliocentric orbits.
I've been playing with a series of tether scenarios. I hope to do the lunar sky hook next.
In your final statement of the V calculation, you have a and r swapped.
Thank you, Anonymous. I did indeed screw up the vis viva equation. I just corrected it.
Post a Comment